In his 1976 article , the late Richard Skemp identifies and explains two meanings for “understanding”, two divergent interpretations of the same word that undoubtably influence everything from pedagogy to policy. (Go here to read David Wees’ thoughtful post about Instrumental and Relational Understanding.) These two meanings co-exist simultaneously with two significantly different interpretations of what math is.
Does this become a self-perpetuating, chicken-egg circle? Which came first? Surely our beliefs about what math is rise out of our own experiences as math learners. If we adhere to those same beliefs as educators, we will teach in the same way in which we were taught, developing in turn the same beliefs in a new generation of learners. The only break in the cycle is when someone, teacher or learner, has an opportunity to experience learning math in an alternative way. And I think this experience needs to be profound enough to at the very least allow you to see that choices exist.
I was fortunate enough to have several such experiences. Here’s my story: When my own children were nearing adulthood, I decided I wanted to become a teacher. I had no clue about what I would teach, but began taking general classes at the local community college that were required to get into a graduate education program. This also meant taking some math classes, and I tested into a level of math about equal to high school Algebra 1. The extent of my prior math education was limited to one year each Algebra and Geometry in high school. No math classes in college. Not required, not interested. Yet I had been an “A” student in math because I was able to successfully imitate what the teacher was doing and did all my assignments, memorizing and performing routine processes and formulas. Nothing more was expected of me. I did not hate it, but I did not love it, either.
So there I was, repeating the algebra content I last ended with, which is when I had the first of a series of eye-opening experiences about math and learning math. One of my instructors was a retired high school teacher, and although he did quite a bit of direct instruction, he also got us talking about WHY, not just how. (Cue heavenly voices.) The moment I recognized that there was so much more to math than imitate-memorize-regurgitate, the moment I realized that math was both beautiful and interesting, was the exact moment I decided to become a math teacher.
I continued devouring math classes (through the first term of calculus) until it was time to begin my grad program. I was no longer satisfied with instrumental understanding, I wanted to really understand relationally (although I did not call it that) so that I could pass that understanding on to my future, oh-so-lucky students. Along the way, I also got a Middle School Math certificate. Through my math and education coursework, I found out that the best learning is learning with others, not next to them. Glorious. That you can (and should) revise your work as you gain new insights, that you can follow more than one solution path, that math ideas are wonderfully interconnected. In Skemp’s words, I was now “able to consider the alternative goals of instrumental and relational understanding on their merits” and choose.
To make an informed choice of this kind implies awareness of the distinction, and relational understanding of the mathematics itself. So nothing else but relational understanding can ever be adequate for a teacher. (R. Skemp)
I totally stole this image from David Wees because I think it is awesome. If I committed a blogging no-no, I’m sure someone will let me know.
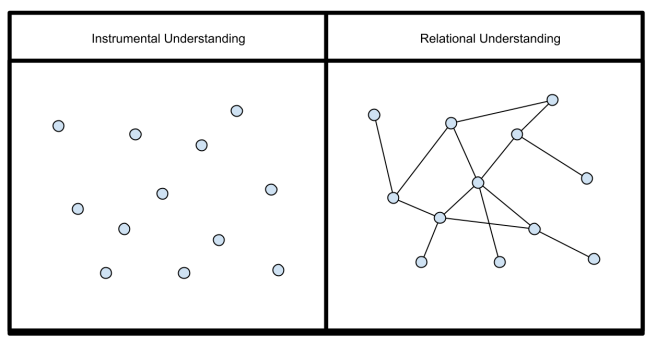
How successful have I been in my endeavors to teach relationally? That’s a whole other post (or three). What do I think relational teaching and learning looks like? I’m working on figuring that out. That’s a whole blog.
Hi Pat,
I like how you connected your experiences with math to this theory of what math is. That kind of narrative is really enticing as a reader.
I am totally cool with you using my picture. You’ve given me credit and I think you’d have a fair use claim anyway.
David
LikeLike
Hi, David,
I am totally blown away at the moment at how we just connected via blogging. This is seriously an emotional, defining moment for me. Just reading what other people wrote was amazing enough; I am so thrilled about the potential here.
Thank you so much for reaching out.
Pat
LikeLike
I can relate so much to your article. As a college student studying math i to go through the motions not really understanding what and why I’m doing what I’m doing. But as soon as that understanding becomes clear maps no longer a chore but it can be fun. I believe this is the key to unlocking young minds into mathematics.
LikeLike
Reblogged this on Mathematical Inquiry 11.
LikeLike